CYCLIC REDUNDANCY CHECK (CRC) -NETWORKING

⧭ Today we will discuss about the technique to find  sequence of redundant bit in any  message. Cyclic Redundancy Checker technique  is used to detecting redundant bit. Let we  know more about CRC (Cyclic Redundancy Checker technique).

CRC GENERATOR:

➧ CRC is redundancy checking technique.

➧ CRC is based on binary division.

➧ In CRC instead of adding bit together to achieve a desired parity , a sequence of redundant bit is called CRC or the CRC remainder is appanded to the end of data unit.So that the resulting data unit become exactly divisible by a second, predetermined binary number.

➧ At its destination the incoming data unit is divided by same number.

➧ If at this step there is no remainder the data unit is assumed to be intact and is therefore accepted.

➧ A remainder indicate that the data unit has been damaged in transit and therefore must be rejected.

➧ CRC must have two qualities:

⧪ It must have one less bit than the divisor.

⧪ Appending it to the end of the data string must make the resulting bit sequence exactly divisible by divisor.

⧭ Let we first understand CRC Generator:

From the above diagram CRC=001

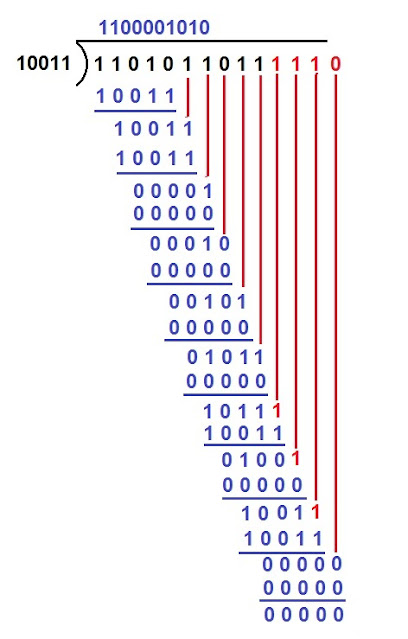
⧭ Let we understand the procedure of finding CRC by the help of above example:

Given :

    ➧Divisor           : 1101

    ➧Data              : 100100

    ➧Quotient        : 111101

    ➧Remainder     : 001

    ➧Method Used  : Binary Division / Modulo-2 division is used

⧭ In this method "000" is used at the end of data part i.e "100100" we get "100100000"

Now the new data is "100100000"

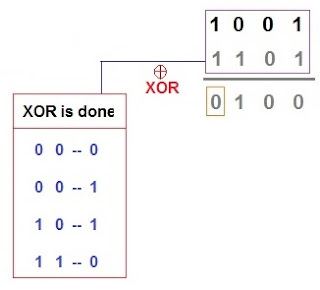
⧭ In this method XOR-ing is used in this division such as:

➧Here after XOR operation between (11001 & 1101) we get "0100" so same method is apply in complete division.

⧭ Note from "0100" left most 0 will we neglected.

➧XOR table is given in above diagram for reference.

A question arise in our mind, why only three 0's are added in data part ? so the formula is:

➧Extra Bit = Divisor bits - 1

⧭ For example here number of bits in divisor is 4 so the extra bit will be (4-1=3) that's why we will add three bit i.e three 0's.

⧭ Note : CRC bit = Remainder i.e what we will get remainder is called  CRC bits.

CRC CHECKER:

⧭ A CRC checker function exactly like the generator. After receiving data appending with the CRC, It does the same modulo-2 division if the remainder is all 0's the CRC is dropped and data is accepted. Otherwise the received stream of bit is discarded and data are resend.

⧭ Let we understand CRC Checker:

➧ In CRC checker the procedure is same as CRC generator but only the change is extra bit. 

➧ Here extra bit will be 001 (what the remainder in CRC generator)

➧ After adding extra bit and modulo-2 division we will get "000" remainder. Which shows no error. In this way by using this method we will remove error from data part.

⧭ GENERATOR POLYNOMIAL (GP):

Example:

1. If G.P = x⁴ + x + 1

                    = 1.x⁴ + 0.x³ + 0.x² + 1.x¹ + 1.x⁰

                          ^{1         0         0        1         1}

         ^{G.P = 10011}

2. If G.P = x⁶ + x² + x + 1

             =1.x⁶ + 0.x⁵ + 0.x⁴ + 0.x³ + 1.x² + 1.x¹ +1.x⁰

                  1         0        0         0          0          1        1

       G.P = 1000011

⧭ Note: In G.P if there are 'n' power then we get (n+1) bit in G.P

➧ Form the above examples we understand how to find G.P bit, it is basically a divisor in modulo -2 divide. 

➧ But if G.P is given in algebraic equation format than how to find G.P bits.

➧ By the procedure we can easily convert algebraic equation format into binary bits.

⧭ Now we take an complete example to understand.

Question: 

    If G.P = 10011

    If  Packet is = 1101011011

Then we first append four 0's in data packet such as: 1101011011 0000

⧭ Note: Here in G.P there are 5 bits so we append four 0's or In G.P polynomial the highest power is 4 so we append four bits. then we divide using modulo -2 divide. 

Than append the remainder bit in Data Packet such as: 1101011011 1110

⧭ Again apply modulo-2 divide :

G.P=10011 ,  Data = 1101011011 1110

⧭ Now this is 100 % divisible by G.P.

⧭ PRACTICE QUESTIONS:

1.  If  Data : x⁹ + x⁸ + x + 1

         G.P   : x³ + x + 1

2.  If  Data : x⁹ + x⁷ + x⁵ + x³ + 1

         G.P   : x³ + 1